Research
My current research focuses on developing causal inference and statistical and machine learning methods for large observational studies, generally, and mobile health data (e.g., accelerometer, heart rate, and GPS tracking data, etc.), specifically. I am especially interested in constructing methods that are both rigorous and flexible such that they are accessible to healthcare professionals and can be tailored to various research questions of interest. More specifics about the data and problems that motivate my current work can be found below.
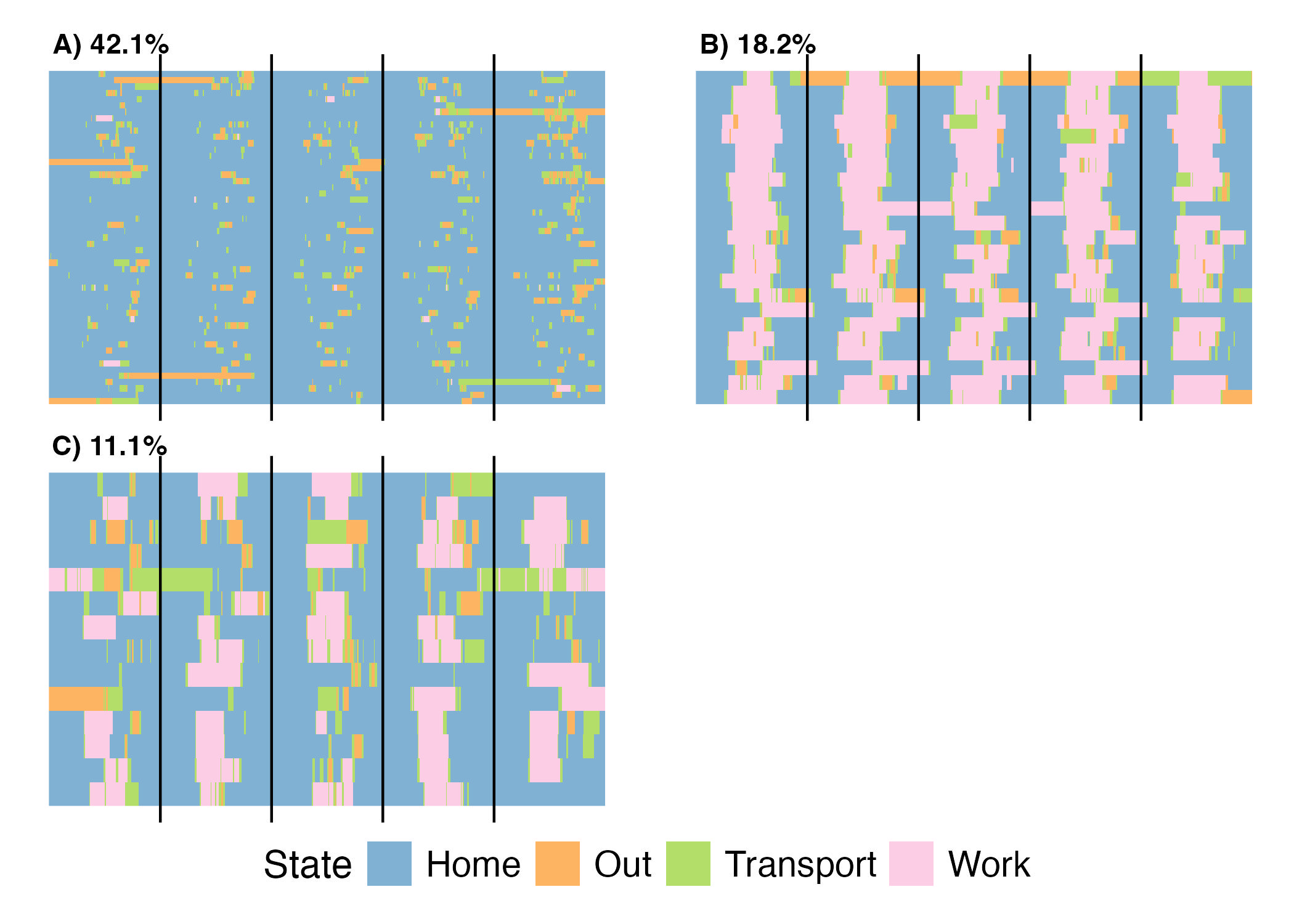
Statistical and machine learning methods for mobile health data
Mobile apps and wearable devices accurately and continuously measure human activity; patterns within this data can provide a wealth of information applicable to fields such as transportation and health. Despite the potential utility of this data, the intensively sampled nature of the data makes it difficult to accomodate the richness of the data without substantially increasing model and/or computational complexity. To adress these challenges, we have proposed a novel clustering method and cluster evaluation metric for human activity data that leverages an adjacency matrix representation to cluster the data without the calculation of a distance matrix. This technique is substantially faster than conventional methods based on computing pairwise distances via sequence alignment algorithms and also enhances interpretability of results. See the corresponding paper for this work here. Furthmore, we are currently working on developing causal inference techniques for functional treatments such that we can explore, for example, how increasing physical activity trajectories in the afternoon impacts human health outcomes.
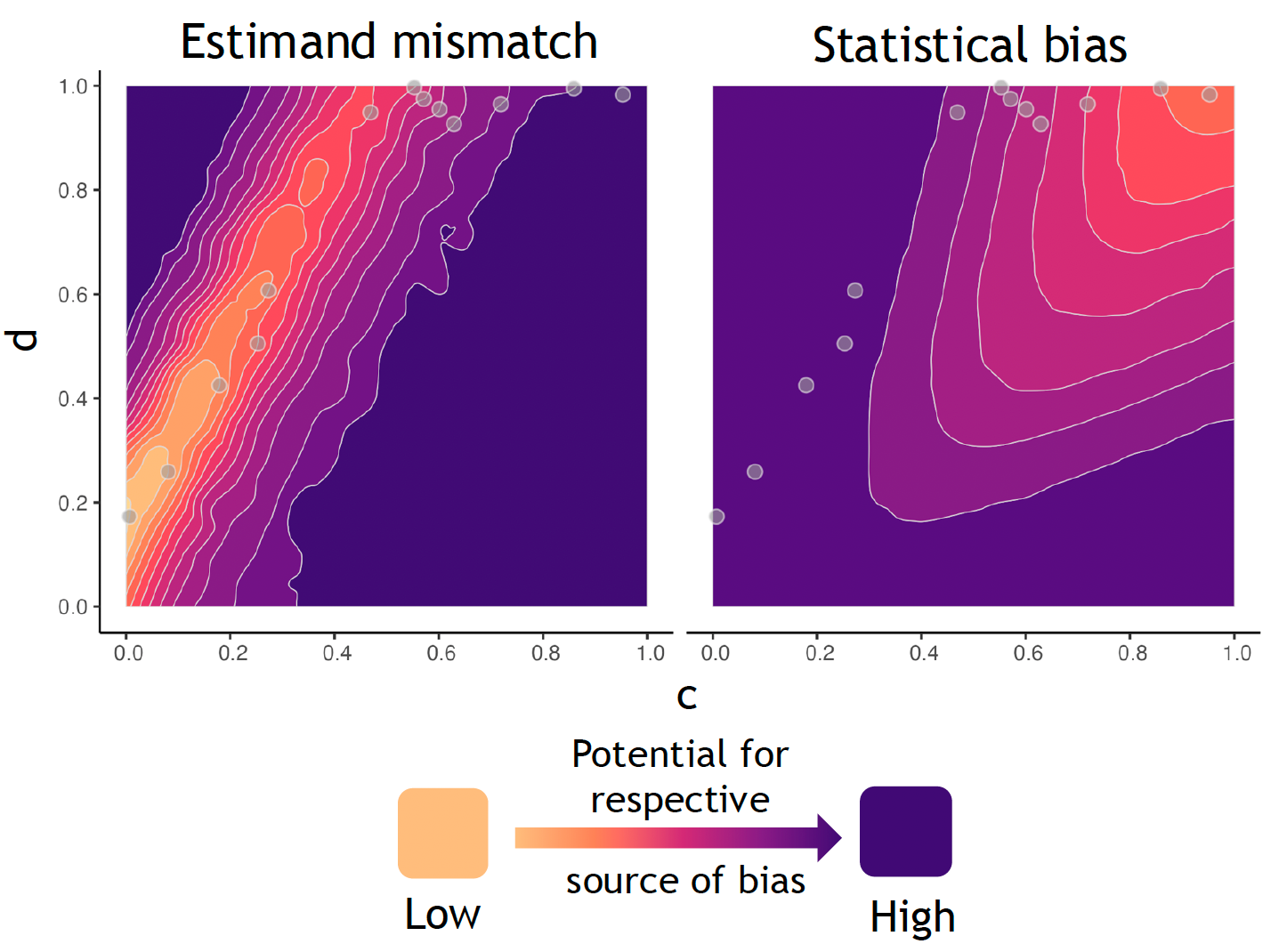
Causal effect estimation under positivity violations
Estimating the causal effect of a binary treatment or health policy with observational data can be challenging due to an imbalance of and a lack of overlap between treated and control covariate distributions. In the presence of limited overlap, researchers choose between 1) methods (e.g., inverse probability weighting) that imply traditional estimands but whose estimators are at risk of considerable bias and variance; and 2) methods (e.g., overlap weighting) which imply a different estimand, thereby modifying the target population to reduce variance. We bridge the gap between these methods by proposing a framework for navigating the tradeoffs between variance and bias due to imbalance and lack of overlap and the targeting of the estimand of scientific interest. This procedure allows analysts to incorporate their domain-specific preference for preservation of the original research population versus reduction of statistical bias when identifying an estimand in scenarios with a lack of overlap. See the corresponding paper for this work here. As an extension of this work, we are currently developing direct balancing weighting methods that yield a solution when there is a lack of overlap by targeting a different population for a subset of covariates.